Knot Theory
Bachelor's Thesis about Knots and the Jones Polynomial
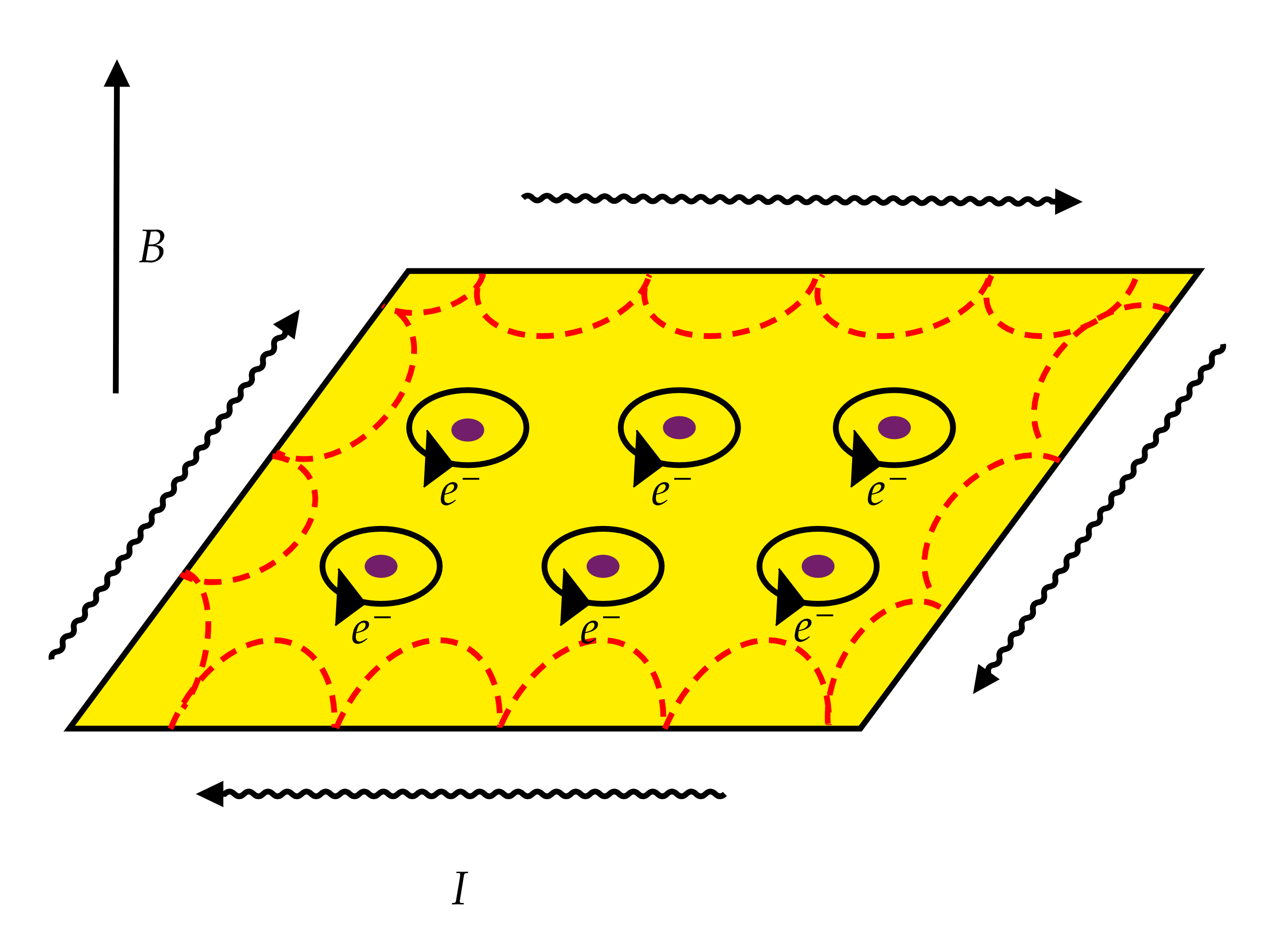
The following PDF, titled Nusos i el polinomi de Jones, is part of my Final Degree Thesis which was done under the supervision of Joan Porti Piqué. In it, I present an introductory study on knot theory, focusing on algebraic invariants, with a special emphasis on the Jones polynomial. I explore how knots can be classified, particularly for lower-order knots, and discuss some applications of knot theory in fields like quantum computing and molecular biology.
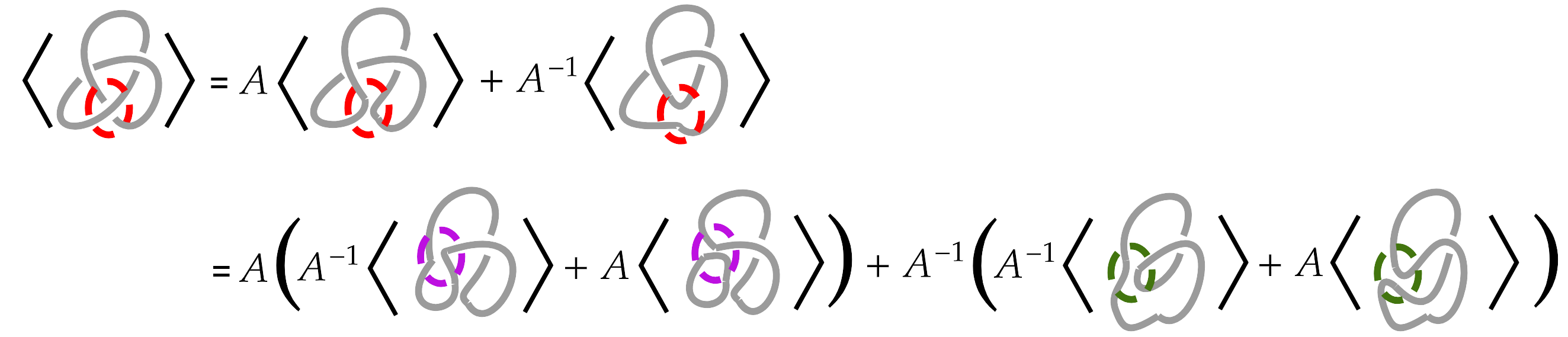
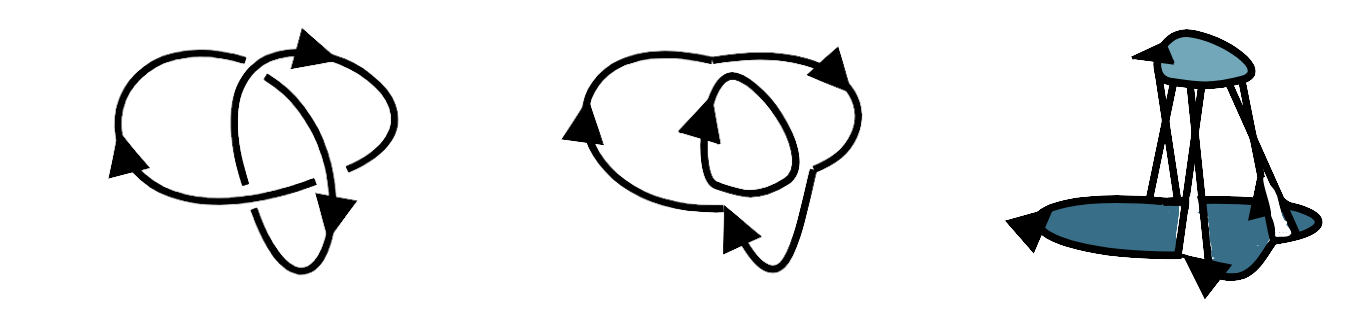
My study begins with a historical overview of knots in human culture and mathematics, explaining their topological properties and key developments in the field. I then introduce fundamental definitions and classifications of knots, highlighting essential concepts such as Reidemeister moves, knot invariants, and the Jones polynomial. In the final sections, I delve into applications, demonstrating the real-world significance of knot theory.
How to Download the Project from GitHub
The document can be found in the following GitHub repository:
🔗 https://github.com/Tutusaus/Knot_Theory
To download the full project, follow these steps:
1. Download as a ZIP File
- Open the repository link in your browser.
- Click on the green “Code” button.
- Select “Download ZIP”.
- Extract the ZIP file on your computer.
2. Clone Using Git (Recommended)
If you have Git installed, open a terminal and run:
git clone https://github.com/Tutusaus/Knot_Theory.git
This will create a local copy of the repository on your computer.
Images